Dilute systems - Chapter 5
Particle free settling
Online free settling velocity calculator for a particle, valid at any reasonable value of Particle Reynolds Number, and not just when within the Stokes's settling regime. The calculator uses the Heywood Table approach for settling velocity calculation when the Particle Reynolds Number is greater than 0.2.
Illustration of the Camp-Hazen model
The Camp-Hazen model uses a 'critical particle trajectory' model for the design of rectangular sedimentation basins,
operating at low solids concentration in the feed, i.e. too low for hindered settling to occur.
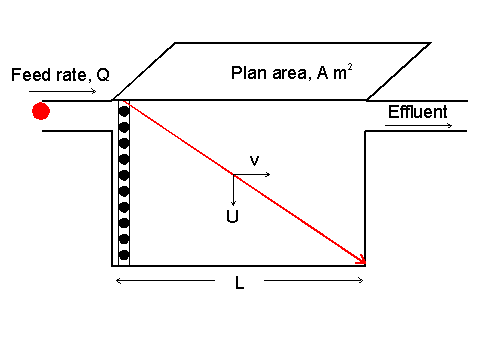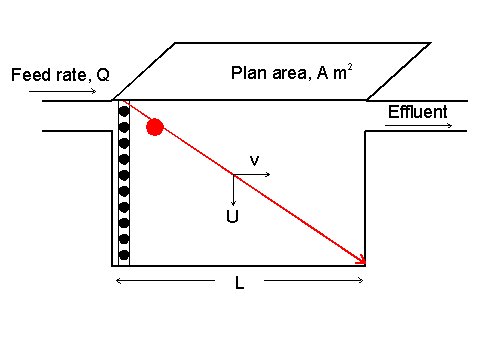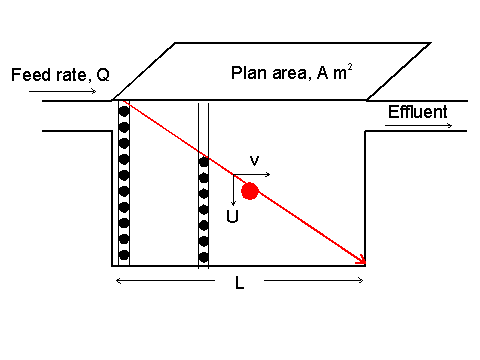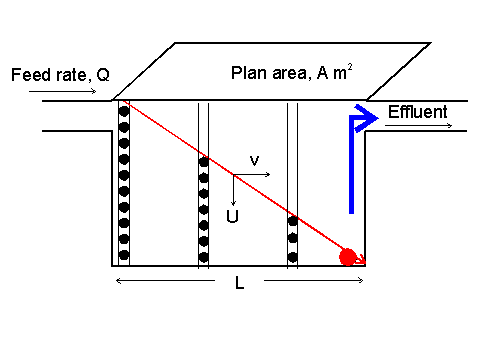
The particle trajectory is one that moves from left-to-right in the same time as it moves from
top-to-bottom of the device. Thus, the residence time horizontally is equal to the residence time vertically. The
assumption is that the particle is just captured onto the base of the vessel prior to the liquid flowing out of the vessel.
The residence time horizontally is the volume of the vessel divided by the volume flow rate of the feed, equal to the
residence time vertically which is the vessel height divided by the terminal settling velocity. Equating these
times gives: Plan Area (of the vessel) multiplied by vessel height over volume flow rate = vessel height over
terminal settling velocity. Cancelling vessel height and rearranging provides the equation for the Plan Area of
the settling vessel is equal to the volume flow rate (Q) divided by the terminal settling velocity (Ut).
The equation thus derived for Plan Area (A)is:
A = Q / U t
This is an important equation, and modelling approach, that is also used in sedimenting centrifuge analysis and
in the capture of dust particles from gases when the gas flow is non-turbulent.
Answers to problems at the end of Chapter 6:
Q1
i) the correct answer is (a)
ii) the correct answer is (b)
iii) log(Px) for the 50, and above, particles are: 0.156, 0.457 and 1.457
log(U/Q) for the 50, and above, particles are: -1.072, -0.513 and 0.759
Settling velocities (by Heywood) are: 0.00243, 0.0088 and 0.165
and by Stokes, for all the sizes: 9.81e-7, 9.81e-5, 0.00245, 0.0098 and 0.98.
iv) Stokes' settling equation only accounts for viscous drag of the fluid around
the particle, the Heywood Tables approach includes drag effects from eddies
and turbulences as well as viscous drag. More drag means the particle will
travel slower - hence Stokes' settling underestimates settling velocity if
significant turbulence is present in the fluid around the particle.
v) the correct answer is (a), obtained by substituting Stokes' settling
equation into the Particle Reynolds number and equating to 0.2; i.e. the
conventional limit of streamline flow of the fluid around the particle.
Q2
i) A parallel trajectory to the critical, but will reach the tank base
before the full tank length.
ii) the correct answer is (a)
iii) the correct answer is (c)
iv) the correct answer is (b)
v) the correct answer is (a)
vi) the correct answer is (b)
vii) square metres and it represents the plan area of the settling tank; i.e.
the area when looking down on the top surface of the tank.
(viii) the correct answer is (b)
Q3
i) the correct answer is (b)
For the rest of this problem, see the linked file here.
FAQ

